🧐Bloom Filter

• 空间效率高的概率型数据结构，用来检查一个元素是否在一个集合中

• 对于一个元素检测是否存在的调用，BloomFilter会告诉调用者两个结果之一：可能存在或者一定不存在

在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

BitMap & Bloom Filter

为减少内存开销，仅仅针对知道是否存在，使用位图算法：

如需求是要根据网页URL（字节数很大）判断网页是否在黑名单：

每个map值都使用1bit，这样大大降低了内存开销，具体做法是，我们使用一个Hash函数将URL映射到大小为n的bit数组中，并置相应位置为True

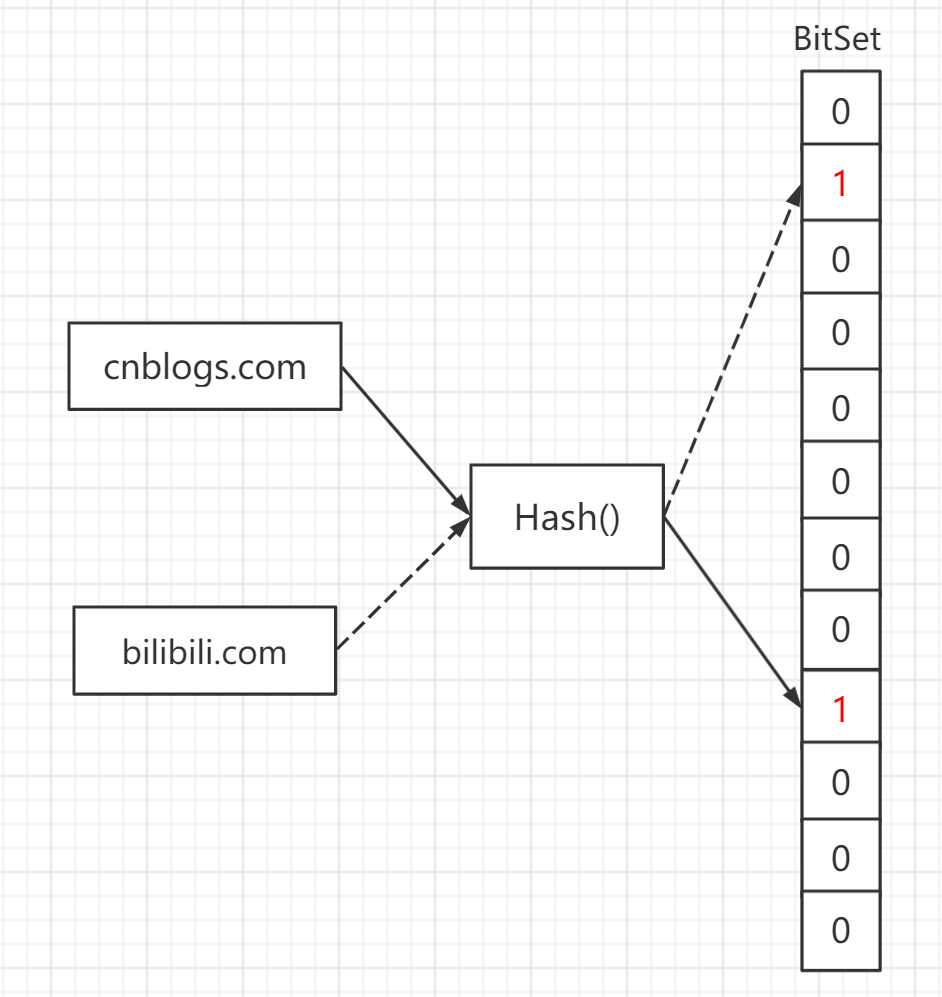
可以在尽可能低的内存开销下，实现O（1）时间的判断URL是否存在黑名单中。

但不得不面对的一个问题就是，即使采取再好的哈希函数，都会出现哈希冲突的情况，在查询阶段出现哈希冲突意味着查询错误，会返回一个错误的结果，而想尽可能的降低哈希冲突，我们需要位图大小比黑名单中URL数量大的多，我们考虑随机哈希的情况下，查询碰撞的概率是：黑名单URL数量/位图大小。所以要想查询准确率高，又带来了更高的内存开销，而可以有效改善这种情况的一种数据结构就是（Bloom Filter）

使用多个Hash函数对数据进行哈希操作（如下图使用了两个hash函数），这样得出多个位置为True，相比位图它在有限的空间内，尽可能的降低了查询失败的可能，这一点可以从信息熵的角度来看，每一个位置所包含的信息更加多了，所以比起位图来说，布隆过滤器对空间的利用率也变大了

image-20210715164606827

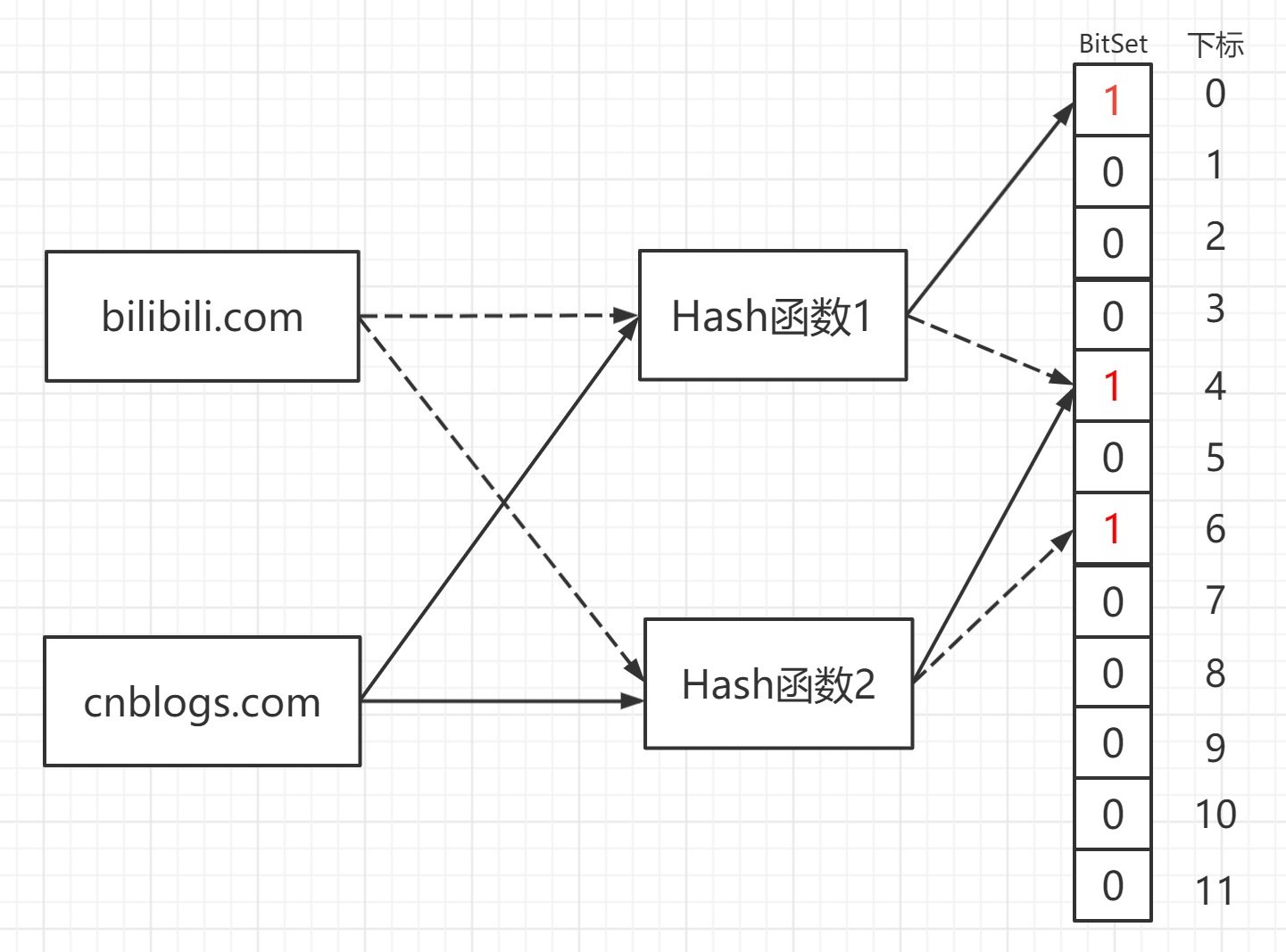
集合表示和元素查询

下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。

img

为了表达S={x1, x2,…,xn}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置hi(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位）。

img

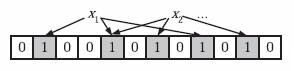
在插入一个元素时，会使用k个hash函数，来计算出k个在bit array中的位置，然后，将bit array中这些位置的bit都置为1

在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有hi(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y1就不是集合中的元素。y2或者属于这个集合，或者刚好是一个false positive

img

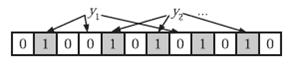
不允许有删除操作，因为删除后，可能会造成原来存在的元素返回不存在，这个是不允许的

不允许删除的机制会导致其中的无效元素可能会越来越多，即实际已经在磁盘删除中的元素，但在bloomfilter中还认为可能存在，这会造成越来越多的false positive，在实际使用中，一般会废弃原来的BloomFilter，重新构建一个新的BloomFilter

如果要布隆过滤器支持删除，那么怎么办呢？

有一个叫做 Counting Bloom Filter:

它用一个 counter 数组替换数组的比特位，这样一比特的空间就被扩大成了一个计数器, 用多占用几倍的存储空间的代价，给 Bloom Filter 增加了删除操作。

但是还有更好的解决方案，那就是布谷鸟过滤器。

对比

常用的数据结构，如hashmap，set，bit array都能用来测试一个元素是否存在于一个集合中

• 对于hashmap，其本质上是一个指针数组，一个指针的开销是sizeof(void *)，在64bit的系统上是64个bit，如果采用开链法处理冲突的话，又需要额外的指针开销，而对于BloomFilter来讲，返回可能存在的情况中，如果允许有1%的错误率的话，每个元素大约需要10bit的存储空间，整个存储空间的开销大约是hashmap的15%左右

• 对于set:

  • 如果采用hashmap方式实现，情况同上

  • 如果采用平衡树方式实现，一个节点需要一个指针存储数据的位置，两个指针指向其子节点，因此开销相对于hashmap来讲是更多的

• 对于bit array，对于某个元素是否存在，先对元素做hash，取模定位到具体的bit，如果该bit为1，则返回元素存在，如果该bit为0，则返回此元素不存在。可以看出，在返回元素存在的时候，也是会有误判的，如果要获得和BloomFilter相同的误判率，则需要比BloomFilter更大的存储空间

劣势：

• 相对于hashmap和set，BloomFilter在返回元素可能存在的情况中，有一定的误判率，这时候，调用者在误判的时候，会做一些不必要的工作，而对于hashmap和set，不会存在误判情况

• 对于bit array，BloomFilter在插入和查找元素是否存在时，需要做多次hash，而bit array只需要做一次hash，实际上，bit array可以看做是BloomFilter的一种特殊情况

以一个例子具体描述使用BloomFilter的场景，以及在此场景下，BloomFilter的优势和劣势。

一组元素存在于磁盘中，数据量特别大，应用程序希望在元素不存在的时候尽量不读磁盘。

• 此时，可以在内存中构建这些磁盘数据的BloomFilter，对于一次读数据的情况，分为以下几种情况：

  • 请求的元素不在磁盘中，如果BloomFilter返回不存在，那么应用不需要走读盘逻辑，假设此概率为P1；如果BloomFilter返回可能存在，那么属于误判情况，假设此概率为P2

  • 请求的元素在磁盘中，BloomFilter返回存在，假设此概率为P3

• 如果使用hashmap或者set的数据结构，情况如下：

  • 请求的数据不在磁盘中，应用不走读盘逻辑，此概率为P1+P2

  • 请求的元素在磁盘中，应用走读盘逻辑，此概率为P3

假设应用不读盘逻辑的开销为C1，走读盘逻辑的开销为C2，那么，BloomFilter 和 hashmap 的开销为

Cost(BloomFilter) = P1 * C1 + (P2 + P3) * C2
Cost(HashMap) = (P1 + P2) * C1 + P3 * C2;

Delta = Cost(BloomFilter) - Cost(HashMap)
      = P2 * (C2 - C1)

因此，BloomFilter 相当于以增加P2 * (C2 - C1)的时间开销，来获得相对于hashmap而言更少的空间开销。

既然P2是影响BloomFilter性能开销的主要因素，那么BloomFilter设计时如何降低概率P2（即false positive probability）呢

参数取值

实际应用关注 false positive，因为和额外开销有关，实际应用中期望给定一个 false positive probability 和将要插入的元素的数量

依然是上文的 m, n, k，false positive probability = p

=> :

如果需要最小化 false positive probability，则k的取值如下（①）

k = m * ln2 / n;  

而p的取值，和m，n又有如下关系（②）

m = - n * lnp / (ln2) ^ 2 

把①代入②，得出给定n和p，k的取值应该为

k = -lnp / ln2

最后，也同样可以计算出m

BloomFilter实现及优化

Basic version

DS:

template <typename T>
class BloomFilter {
    public:
    BloomFilter(const int32_t n, const double false_positive_p);
    void insert(const T &key);
    bool key_may_match(const T &key);
    
    private:
    std::vector<char> bits_; // 模仿bit array
    int32_t k_;
    int32_t m_;
    int32_t n_;
    double p_;
}

// init:
template <typename T>
BoomFilter<T>::BoomFilter(const int32_t n, const double false_positive_p)
    : bits_(), k_(0), m(0), n_(n), p_(false_positive_p) {
        k_ = static_cast<int32_t>(-std::log(p_) / std::log(2));
        m_ = static_cast<int32_t>(k_ * n * 1.0 / std::log(2));
        bits_.resize((m_ + 7) / 8, 0);
}

// insert:
// 设置每个hash函数计算出来的bit为1
template<typename T>
void BloomFilter<T>::insert(const T &key) {
  uint32_t hash_val = 0xbc9f1d34;
  for (int i = 0; i < k_; ++i) {
    hash_val = key.hash(hash_val);
    const uint32_t bit_pos = hash_val % m_;
    bits_[bit_pos/8] |= 1 << (bit_pos % 8);
  }    
}
    
// check
// 计算每个hash函数对应的bit的值，如果全为1，则返回存在；否则，返回不存在
template<typename T>
bool BloomFilter<T>::key_may_match(const T &key) {
  uint32_t hash_val = 0xbc9f1d34;
  for (int i = 0; i < k_; ++i) {
    hash_val = key.hash(hash_val);
    const uint32_t bit_pos = hash_val % m_;
    if ((bits_[bit_pos / 8] & (1 << (bit_pos % 8))) == 0) {
      return false;
    }
  }
  return true;
}

整个BloomFilter包含三个操作：

• 初始化：即上述代码中的构造函数

• 插入：即上述代码中的insert

• 判断是否存在：即上述代码中的key_may_match

Optimization

多次调用了hash_func函数，这对于计算比较长的字符串的hash的开销是比较大的

多次调用了hash_func函数，这对于计算比较长的字符串的hash的开销是比较大的

可以采用两次hash的方式来替代上述的多次的计算:

例如insert_optimized:

template<typename T>
void BloomFilter<T>::insert2(const T &key) {
    uint32_t hash_val = key.hash(0xbc9f1d34); // 1st
    const uint32_t delta = (hash_val >> 17) | (hash_val << 15); // 2nd
    for (int i = 0; i < k; ++i) {
        const uint32_t bit_pos = hash_val % m_;
        bits_[bit_pos/8] |= 1 << (bit_pos % 8);
        hash_val += delta;
    }
}

先用通常的hash函数计算一次，然后，使用移位操作计算一次，最后，k次计算的时候，不断累加两次的结果

优化后，最大的false positive probability增长，可以增加k来弥补，因为优化后的hash算法，在k增长时，带来的开销相对来讲不大

P.S.:

int_t 为一个结构的标注，可以理解为type/typedef的缩写，表示它是通过typedef定义的，而不是一种新的数据类型。因为跨平台，不同的平台会有不同的字长，所以利用预编译和typedef可以最有效的维护代码

• int8_t : typedef signed char;

• uint8_t : typedef unsigned char;

• int16_t : typedef signed short ;

• uint16_t : typedef unsigned short ;

• int32_t : typedef signed int;

• uint32_t : typedef unsigned int;

• int64_t : typedef signed long long;

• uint64_t : typedef unsigned long long;

size_t与ssize_t

size_t主要用于计数，如sizeof()函数返回值类型即为size_t,在不同位的机器中所占的位数也不同

size_t是无符号数，ssize_t是有符号数。

在32位机器中定义为：typedef unsigned int size_t; （4个字节） 在64位机器中定义为：typedef unsigned long size_t;（8个字节）

由于size_t是无符号数，因此，当变量有可能为负数时，必须使用ssize_t:

因为当有符号整型和无符号整型进行运算时，有符号整型会先自动转化成无符号

四种类型转换运算符

关键字	说明
static_cast	用于良性转换，一般不会导致意外发生，风险很低： 原有的自动类型转换, void 指针和具体类型指针之间的转换, 有转换构造函数或者类型转换函数的类与其它类型之间的转换，不过static_cast 不能用于无关类型之间的转换（两个具体类型指针之间的转换、int 和指针之间的转换），转换失败的话会抛出一个编译错误；
const_cast	用于 const 与非 const、volatile 与非 volatile 之间的转换。
reinterpret_cast	高度危险的转换，这种转换仅仅是对二进制位的重新解释，不会借助已有的转换规则对数据进行调整，但是可以实现最灵活的 C++ 类型转换。可以认为是 static_cast 的一种补充，一些 static_cast 不能完成的转换，就可以用 reinterpret_cast 来完成，例如两个具体类型指针之间的转换、int 和指针之间的转换（有些编译器只允许 int 转指针，不允许反过来）
dynamic_cast	借助 RTTI，用于类型安全的向下转型（Downcasting）;与 static_cast 是相对的，dynamic_cast 是“动态转换”的意思，static_cast 是“静态转换”的意思。dynamic_cast 会在程序运行期间借助 RTTI 进行类型转换，这就要求基类必须包含虚函数，类向上转型是安全的（父类转子类），不做解释，向下转型不安全：每个类都会在内存中保存一份类型信息，编译器会将存在继承关系的类的类型信息使用指针“连接”起来，从而形成一个继承链：同一个类的不同对象指向同一个类型信息，有继承关系的类型信息组成一条链。当使用 dynamic_cast 对指针进行类型转换时，程序会先找到该指针指向的对象，再根据对象找到当前类（指针指向的对象所属的类）的类型信息，并从此节点开始沿着继承链向上遍历，如果找到了要转化的目标类型，那么说明这种转换是安全的，就能够转换成功，如果没有找到要转换的目标类型（直到继承链的顶点（最顶层的基类）还没有遇到），那么说明这种转换存在较大的风险，就不能转换。

这四个关键字的语法格式都是一样的，具体为：

xxx_cast<newType>(data)

newType 是要转换成的新类型，data 是被转换的数据