# Cuckoo Filter：Better Than Bloom

布隆过滤器有缺点，比如不支持删除操作、查询效率弱，因为多个随机哈希函数探测的是bit数组中多个不同的点，所以会导致低CPU缓存命中率

**乐，我就是比你弔：**

![img](https://s2.loli.net/2022/07/24/OSfnMs3leCuqTpU.png)

`Cukoo`解决了这个问题：用**更低的空间开销**解决了布隆过滤器**不能删除元素**的问题

* supports adding and removing items dynamically （动态的添加和删除元素）
* higher lookup performance, even when close to full （更高的查找性能，即使在接近满的情况下）
* easier to implement than alternatives such as the quotient filter （比起商过滤器它更容易实现）
* less space if the target false positive rate is less than 3% （如果要求误判率低于3%，它比布隆过滤器有更低的空间开销）

贴一个[***CMU的佬写的C++实现👈***](https://github.com/efficient/cuckoofilter)

## **Cuckoo Hash**

最原始的布谷鸟哈希方法是使用两个哈希函数对一个`key`进行哈希，得到桶中的两个位置，此时

* 如果两个位置都为为空则将`key`随机存入其中一个位置
* 如果只有一个位置为空则存入为空的位置
* 如果都不为空，则随机踢出一个元素，踢出的元素再重新计算哈希找到相应的位置

当然假如存在绝对的空间不足，那老是踢出也不是办法，所以一般会设置一个**踢出阈值**，如果在某次插入行为过程中连续踢出超过阈值，则进行扩容。

![image-20210727104910960](https://s2.loli.net/2022/07/24/4URBirfyup3SGVm.png)

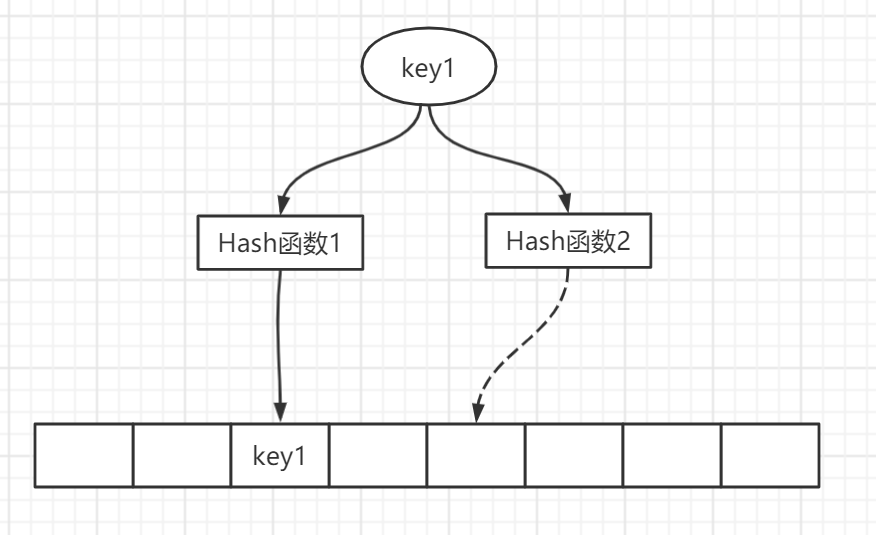
***换言之：***

![img](https://s2.loli.net/2022/07/24/h5TSCN4qmMRQ7jK.png)

它有两个 hash 表，记为 T1，T2。

两个 hash 函数，记为 h1，h2。

当一个不存在的元素插入的时候，会先根据 h1 计算出其在 T1 表的位置，如果该位置为空则可以放进去。

如果该位置不为空，则根据 h2 计算出其在 T2 表的位置，如果该位置为空则可以放进去。

如果该位置不为空，就把当前位置上的元素踢出去，然后把当前元素放进去就行了。

也可以随机踢出两个位置中的一个，总之会有一个元素被踢出去。

被踢出去的元素怎么办呢？

![img](https://s2.loli.net/2022/07/24/ivVhZclT2Kqrjxu.png)

![img](https://s2.loli.net/2022/07/24/k9YiWG7tVD5nahw.png)

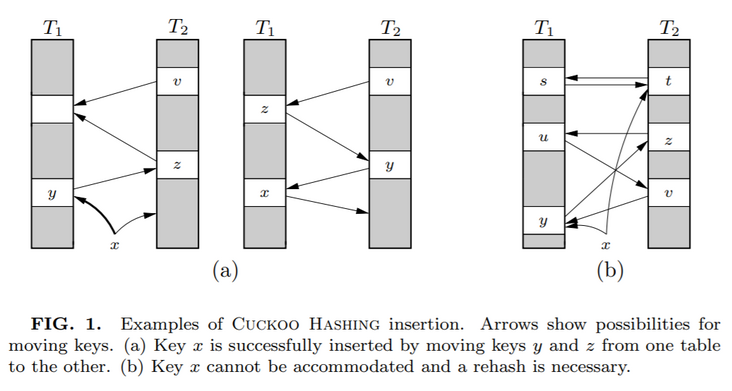
这种类似于套娃的解决方式看是可行，但是总是有出现**循环踢出**导致放不进 x 的问题。

比如上图中的(b)

当遇到这种情况时候，说明布谷鸟 hash 已经到了极限情况，应该进行扩容，或者 hash 函数的优化。所以，你再次去看伪代码的时候，你会明白里面的 `MaxLoop` 的含义是什么了。

这个 `MaxLoop` 的含义就是为了避免相互踢出的这个过程执行次数太多，设置的一个阈值。

## **Cuckoo Filter**

![1](https://s2.loli.net/2022/07/24/YeU32Z8WGgjxaqh.jpg)

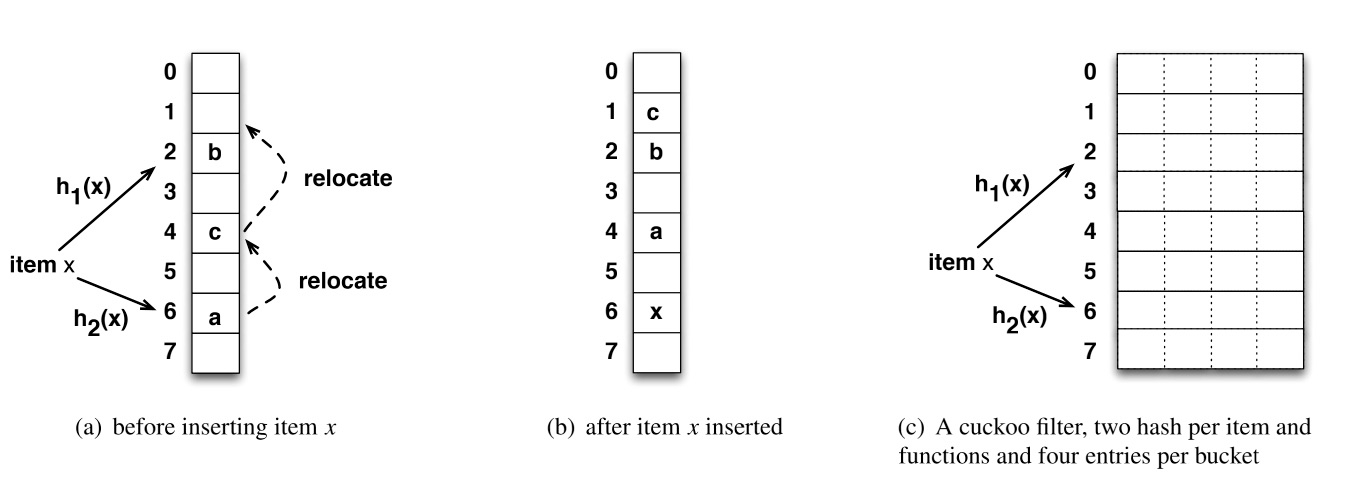
（a）(b)展示了一个基本的**布谷鸟哈希表的插入**操作，是由一个**桶数组**组成，每个插入项都有由**散列函数`h1(x)`和`h2(x)`确定的两个候选桶**，具体操作上文中已经描述。

而基本的布谷鸟过滤器也是由两个或者多个哈希函数构成，布谷鸟过滤器的布谷鸟哈希表的基本单位称为**条目（entry）**。 **每个条目存储一个指纹（fingerprint）**。

指纹指的是使用一个哈希函数生成的n位比特位，n的具体大小由所能接受的误判率来设置，论文中的例子使用的是\*\*`8 bits`\*\*的指纹大小。

查询数据的时候，就是看看对应的位置上有没有对应的“指纹”信息：

![img](https://s2.loli.net/2022/07/24/i57bxQrg8Ukhs16.png)

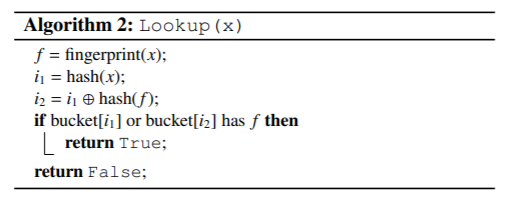
删除数据的时候，也只是抹掉该位置上的“指纹”而已：

![img](https://s2.loli.net/2022/07/24/e7lcZzRQypOBakj.png)

由于是对元素进行 hash 计算，那么必然会出现“指纹”相同的情况，也就是会出现误判的情况。

没有存储原数据，所以牺牲了数据的准确性，但是只保存了几个 bit，因此提升了空间效率。

前面的(a)、(b)很简单，还是两个 hash 函数，但是没有用两个数组来存数据，就是基于一维数组的布谷鸟 hash ，核心还是踢来踢去，重点在于(c)，对数组进行了展开，从一维变成了二维：每一个下标，可以放 4 个元素了，空间利用率飙升！

\_**缺点**\_详见论文第六节or**本文下面**

### **Insert**

插入是重点，与朴素的布谷鸟哈希不同。首先，我们回忆一下布谷鸟 hash，它存储的是插入元素的原始值，比如 x，x 会经过两个 hash 函数，如果我们记数组的长度为 L，那么就是这样的：

`p1 = hash1(x) % L`

`p2 = hash2(x) % L`

***

布谷鸟过滤器采取了两个并不独立的哈希函数:

先说指纹：具体的指纹是通过哈希函数取一定量的比特位:

`f = fingerprint(x)`

下面是哈希函数：

`i1 = h1(x) = hash(x)` 通过某个哈希函数计算出来

`i2 = h2(x) = i1 ⊕ hash(f)` 使用第一个索引和**指纹的哈希**做了一个异或操作

`i1`、`i2`即计算出来两个**桶的索引**。进行异或操作是因为异或操作的特性：同为0不同为1，且**0和任何数异或是这个数的本身**。异或运算确保了一个重要的性质：位置 i2 可以通过位置 i1 和 i1 中存储的“指纹”计算出来，即：**在桶中迁走一个键，我们直接用当前桶的索引`i`和存储在桶中的指纹计算它的备用桶**。

**因为使用的异或运算，所以这两个位置具有对偶性。**

只要保证 **hash(x’s fingerprint) !=0**，那么就可以确保 h2!=h1，也就可以确保，不会出现自己踢自己的死循环问题。

**为什么不直接用索引1和指纹做异或操作**：因为指纹一般只是**key映射出来的少量bit位置**，那么假如不进行哈希操作，当指纹的比特位与整个桶数组相比很小时，那么备用位置使用“**i ⊕ 指纹**”，将被放置到离桶`i1`很近的位置，比如使用八位的指纹大小，最多只能改变`i1`的低八位，所以也就是两个候选通的位置最多相差256，不利于均匀分配。

所以，对“指纹”进行哈希处理可确保被踢出去的元素，可以重新定位到哈希表中完全不同的存储桶中，从而减少哈希冲突并提高表利用率。

***还有个问题：***

它没有对数组的长度进行取模，那么它怎么保证计算出来的下标一定是落在数组中的呢？

这个就得说到布谷鸟过滤器的另外一个限制了：

其**强制数组的长度必须是 2 的指数倍**：二进制一定是这样的：10000000...（n个0）。

这个限制带来的好处就是，进行异或运算时，可以保证计算出来的下标一定是落在数组中的。

这个限制带来的坏处就是：

> * 布谷鸟过滤器：我支持删除操作。
> * 布隆过滤器：我不需要限制长度为 2 的指数倍。
> * 布谷鸟过滤器：我查找性能比你高。
> * 布隆过滤器：我不需要限制长度为 2 的指数倍。
> * 布谷鸟过滤器：我空间利用率也高。
> * 布隆过滤器：我不需要限制长度为 2 的指数倍。
> * 布谷鸟过滤器：我烦死了，CNM！

### **Search**

给定一个项x，算法首先根据上述插入公式，计算x的指纹和两个候选桶。然后读取这两个桶：如果两个桶中的**任何现有指纹匹配**，则布谷鸟过滤器返回true，否则过滤器返回false。此时，只要不发生桶溢出，就可以确保没有假阴性

### **Delete**

标准布隆过滤器不能删除，因此删除单个项需要重建整个过滤器，而计数布隆过滤器需要更多的空间。

布谷鸟过滤器就像计数布隆过滤器，可以通过从哈希表删除相应的指纹从而删除插入的项，其他具有类似删除过程的过滤器比布谷鸟过滤器更复杂。

具体删除的过程也很简单，检查给定项的两个候选桶；如果任何桶中的指纹匹配，则从该桶中删除匹配指纹的一份副本。

## **缺点**

* \*\*删除不完美，存在误删的概率。\*\*删除的时候只是删除了一份指纹副本，并不能确定此指纹副本是要删除的key的指纹。同时这个问题也导致了假阳性的情况。
* \*\*插入复杂度比较高。\*\*随着插入元素的增多，复杂度会越来越高，因为存在桶满，踢出的操作，所以需要重新计算，但综合来讲复杂度还是常数级别。
* **存储空间的大小必须为2的指数**的限制让空间效率打了折扣。
* **同一个元素最多插入kb次**，（k指哈希函数的个数，b指的桶中能装指纹的个数也可以说是桶的尺寸大小（一个下标能放几个元素））如果布谷鸟过滤器支持删除，则必须存储同一项的多个副本。 插入同一项kb+1次将导致插入失败。 这类似于计数布隆过滤器，其中重复插入会导致计数器溢出。

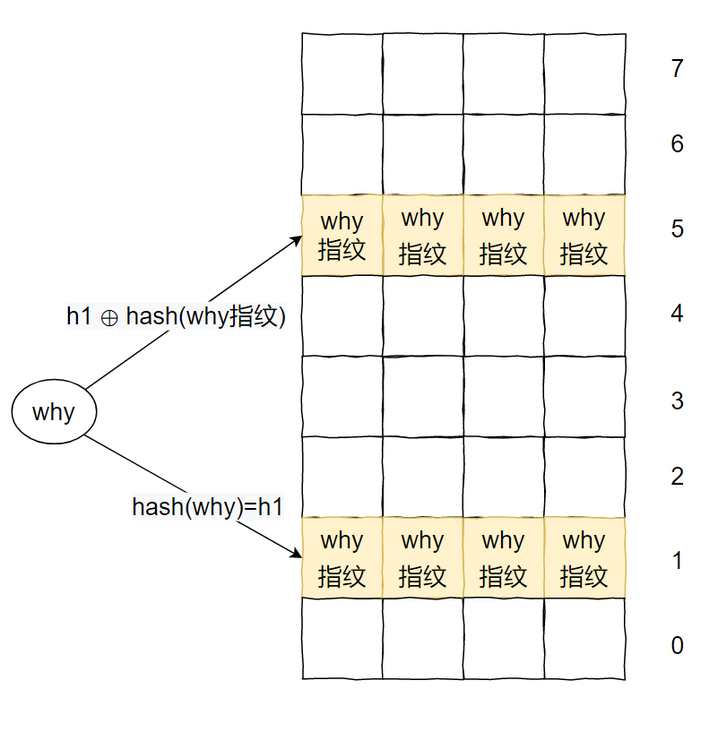
  比如 2 个 hash 函数，一个二维数组，它的每个下标最多可以插入 4 个元素。那么对于同一个元素，最多支持插入 8 次。

  例如下面这种情况：

  why 已经插入了 8 次了，如果再次插入一个 why，则会出现循环踢出的问题，直到最大循环次数，然后返回一个 false。

  怎么避免这个问题呢

  我们维护一个记录表，记录每个元素插入的次数就行了。

  虽然逻辑简单，但是想想数据量大的情形，这个表的存储空间又怎么算呢？emmmmmm

![](https://s2.loli.net/2022/07/24/e9Gqcy4o7AbdXQk.png)

**桶的尺寸**：

是指每个桶能放的指纹个数，保持布谷鸟过滤器的总大小（桶数组）不变，但改变桶的大小（上述例子使用的是大小为4）会导致两个后果：

**(1)** **较大的桶可以提高表的利用率**(即b越大假阳性率越大) ，使用k=2个哈希函数时，当桶大小b=1（即直接映射哈希表）时，负载因子α为50%，但使用桶大小b=2、4或8时则分别会增加到84%、95%和98%。

**(2)** **较大的桶需要较长的指纹才能保持相同的假阳性率**(即b越大f越大)。 使用较大的桶时，每次查找都会检查更多的条目，从而有更大的概率产生指纹冲突。

所以要基于以上寻找一个最合适的桶大小